What Does Newton’s Second Law Say?
Deriving Newton’s Second Law Formula is a powerful exercise that helps us understand one of the most fundamental principles in physics. The law states:
“The force acting on an object is equal to the mass of the object times its acceleration.”
This law gives us a clear mathematical relationship between force, mass, and acceleration. Every time you see something speed up, slow down, or change its direction, this law is at work. If you’re new to this concept, catch up with our overview: Newton’s Second Law of Motion Explained.


Let’s Begin: Deriving Newton’s Second Law Formula
To understand the formula, let’s go step-by-step.
Force, Mass, and Acceleration
- Force (F): Is what causes an object to move faster, slower, or change its path. It’s a push or a pull.
- Mass (m): Is the amount of matter an object contains. It’s a measure of an object’s inertia (its resistance to changes in motion).To better understand this relationship, you can read more about mass and inertia.
- Acceleration (a): Is the rate at which the object’s velocity changes — this could be speeding up, slowing down, or changing direction.
Newton observed two important things, which are key to deriving Newton’s Second Law Formula:
✅ Increasing force increases acceleration (for a constant mass). If you push something harder, it speeds up faster. ✅ Increasing mass decreases acceleration (for a constant force). If an object is heavier, it accelerates less with the same push.
That’s why mathematically:
- Force is directly proportional to acceleration: Fproptoa
- Force is also directly proportional to mass: Fproptom
Combining Both Proportionalities
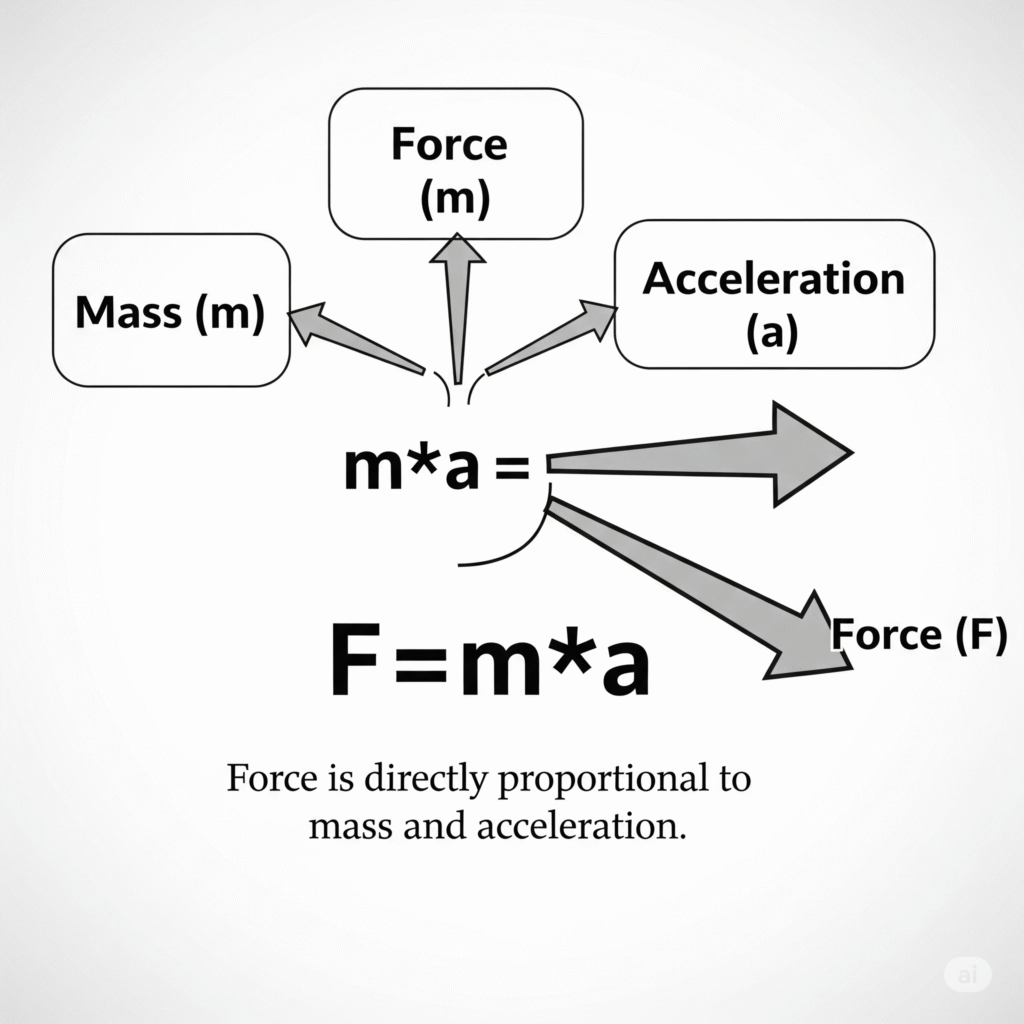
When you put these two observations together, you find that force is proportional to the product of mass and acceleration:
F∝m×a
And to remove the proportionality, we introduce a constant, typically denoted as k. In the International System of Units (SI units), this constant k is defined as 1. This simplification makes the formula elegant and direct:
F=m×a
And there it is — the famous formula of Newton’s Second Law, fully derived! This derivation underpins all calculations involving force, mass, and acceleration.
Understanding the Units
To use the formula correctly, it’s crucial to understand the standard SI units for each quantity:
| Quantity | Symbol | SI Unit |
| Force | F | Newton (N) |
| Mass | m | Kilogram (kg) |
| Acceleration | a | meters per second² (m/s²) |
💡 1 Newton is specifically defined as the force needed to accelerate 1 kilogram (kg) of mass by 1 meter per second squared (m/s²).
Formula in Use: A Quick Example
Let’s put this into practice to see how easy it is to use the formula once you’ve understood deriving Newton’s Second Law Formula. Imagine you have:
- Mass (m) = 2 kg
- Acceleration (a) = 3 m/s²
Using the formula:
F=m×a=2 kg×3 m/s2=6 N
That means you’d need a force of 6 newtons to make a 2 kg object accelerate at 3 m/s².
Quick Tip
Always remember these core relationships, which are the fundamental ideas behind deriving Newton’s Second Law Formula:
- ✅ If force increases (and mass stays the same), acceleration increases—you move faster.
- ✅ If mass increases (and force stays the same), acceleration decreases—it’s harder to move heavier objects.
- ✅ If mass increases, you need more force to get the same acceleration—it’s harder to move heavier objects quickly.
Summary
Deriving Newton’s Second Law Formula (F=m×a) is a powerful tool for understanding motion. Its simple elegance allows us to predict and control how objects move when we apply force. Whether you’re pushing a shopping cart, launching a rocket into space, or observing any change in motion, this law is at the core of the physics that make it happen. This derivation underpins all such calculations and helps you calculate exactly how much force is needed.
Ready to Explore More?
Now that you’ve mastered deriving Newton’s Second Law Formula, next time you use force to move something — be it pushing a chair, lifting weights, or riding a bicycle — take a moment to appreciate the amazing math behind it. Newton’s laws help us explain motion across every scale, and knowing them can give you a deeper appreciation of the world around you.
If you found this guide helpful, be sure to explore more in our Physics Made Easy series.
Stay curious. Stay scientific.



